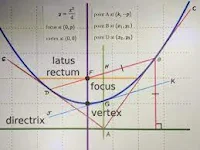
Definition: A parabola is a symmetric curve formed by the set of all points that are equidistant from a fixed line (the directrix) and a fixed point (the focus). Its equation in standard form depends on whether it opens upwards or downwards, or sideways.

Parabola Calculator

Coefficient 'a': Coefficient 'b':

Continue Definition: Here's the standard form equation:

Vertical Parabola (opens upwards or downwards):

Equation: 𝑦=𝑎𝑥**2+𝑏𝑥+𝑐

where a, b, and c are constants, and 𝑎≠0

Horizontal Parabola (opens sideways):

Equation: 𝑥=𝑎𝑦**2+𝑏𝑦+𝑐

where a, b, and c are constants, and 𝑎≠0

For vertical parabolas: If 𝑎>0, the parabola opens upwards.

If a<0, the parabola opens downwards.

For horizontal parabolas: If a>0, the parabola opens to the right.

If a<0, the parabola opens to the left.

Understanding the basic properties of the coefficients

a, b, and c can help users grasp how the parabola is shaped and positioned.

Example:

One practical example of a parabola is the trajectory of a projectile under the influence of gravity. When an object is launched into the air at an angle, its path follows a parabolic shape due to the force of gravity acting on it.

Let's consider the example of a ball being thrown into the air. The path of the ball can be modeled by a vertical parabola. If we neglect air resistance, the equation of its trajectory can be expressed as:𝑦=𝑎𝑥**2+𝑏𝑥+𝑐

where : y represents the vertical position of the ball, x represents the horizontal position of the ball,

a is a constant determined by the initial velocity and angle of projection,

b is the horizontal velocity of the ball (which remains constant if air resistance is ignored)

c is the initial height from which the ball is thrown.

This parabolic trajectory shows the ball rising, reaching its maximum height, and then falling back to the ground. The shape of the trajectory is symmetric, with the highest point of the trajectory occurring at the vertex of the parabola.

This practical example demonstrates how parabolas are not just abstract mathematical concepts, but can be used to describe real-world phenomena, helping us understand and predict the behavior of objects in motion.

Usefullness of Parabola:

Satellite Dishes: The shape of satellite dishes is based on a parabolic curve. This design helps to collect and focus electromagnetic signals from satellites, ensuring efficient transmission of TV, internet, and other communication signals.

Flashlights and Headlights: Some flashlights and headlights utilize parabolic reflectors to focus and direct light beams. The parabolic shape helps in concentrating the light in a specific direction, enhancing brightness and visibility.

Solar Cookers: Parabolic solar cookers use the reflective properties of a parabolic mirror to concentrate sunlight onto a cooking vessel placed at the focal point. This method harnesses solar energy efficiently for cooking and other heating purposes.

Reflecting Telescopes: Many telescopes, including some of the most powerful ones in the world, use parabolic mirrors to gather and focus light from distant celestial objects. The parabolic shape allows for precise imaging and magnification.

Architectural Design: The graceful curve of a parabola is often incorporated into architectural designs to create aesthetically pleasing structures such as bridges, arches, and even buildings. The shape offers strength and stability while adding an elegant touch to the design.

Projectile Motion: Parabolic trajectories are observed in projectile motion, such as the path of a thrown ball or a launched projectile. Understanding the mathematics of parabolas helps in predicting and analyzing the motion of objects in various scenarios, from sports to engineering.

Sound Reflection: In acoustics, parabolic shapes are utilized to reflect and focus sound waves, enhancing the quality and reach of sound in applications like megaphones and certain types of speakers.

Antenna Design: Parabolic antennas are commonly used in telecommunications and broadcasting for transmitting and receiving radio signals. The concave shape of the antenna helps to focus the signal in a specific direction, improving communication efficiency.

Water Fountains: Some water fountains feature parabolic shapes in their design, allowing water to be propelled upwards in an elegant arc. The curvature of the parabola contributes to the aesthetic appeal and functionality of the fountain.

Sporting Equipment: Parabolic shapes are incorporated into the design of sporting equipment such as ski ramps and snowboard halfpipes. These shapes optimize performance by providing smooth, predictable trajectories for athletes.

These applications illustrate the versatility and importance of parabolic curves in various fields, from technology and engineering to architecture and design.

HOW TO EARN MONEY UTLIZING PARABOLA CALCULATOR:

Here are some ways you could monetize a Parabola Calculator:

Subscription Model: Offer premium features such as advanced graphing options, equation solving, and step-by-step solutions for a monthly or yearly subscription fee.

In-App Purchases: Provide additional tools or functionalities as in-app purchases, such as the ability to export graphs as high-resolution images or access to a library of pre-built parabola equations.

Ads: Integrate advertisements within the app, either as banners or interstitials, to generate revenue from user traffic. Freemium Model: Offer a basic version of the app for free with limited features, and then upsell users on a premium version with more advanced capabilities.

Affiliate Marketing: Partner with educational websites or online tutoring services and earn commissions for referring users to their platforms.

White Labeling: License your Parabola Calculator technology to other educational or math-focused apps, earning royalties or upfront fees for each integration.

Educational Resources: Create and sell educational materials such as ebooks, video courses, or interactive tutorials that complement the Parabola Calculator and help users deepen their understanding of parabolas and related concepts.

Consulting Services: Offer personalized consulting or tutoring services to individuals or educational institutions seeking assistance with parabola-related problems or math curriculum development.

Sponsorships: Seek sponsorships from math-related companies or educational institutions to promote their products or services within the app in exchange for financial support.

Crowdfunding: Launch a crowdfunding campaign to raise funds for further development of the Parabola Calculator or to introduce new features based on user feedback.

Each of these strategies has its pros and cons, so it's essential to consider your target audience, the value proposition of your app, and your long-term business goals when deciding on the best monetization approach.

EARN MONEY USING PARABOLA CALCULATOR