Geometric design in transportation engineering:Free Online Tool

Definition: Geometric design in transportation engineering refers to the process of designing the alignment and dimensions of roads, highways, and railways to ensure safe and efficient movement of vehicles. If the superelevation for a curve would be approximately 0.917%, meaning the outer edge of the curve would be elevated by that percentage compared to the inner edge.

Click the Translate button(see right) on this post to set your Own Language to understand more perfectly!!

Geometric Design Of Curvature Calculator

Radius (in meters):

Design Speed (in km/h):

Superelevation (in %):

Result:

Definition continue... Geometric design in transportation engineering refers to the process of designing the alignment and dimensions of roads, highways, and railways to ensure safe and efficient movement of vehicles. This design involves various factors, including radius, speed, and superelevation.

1. **Radius**: The radius of a curve in a road or railway refers to the curvature of that curve. It's measured from the center of the circle that best fits the curve. The radius affects the comfort and safety of vehicles traveling along the curve. A larger radius allows for higher speeds and smoother travel.

2. **Speed**: Speed is the rate at which an object moves along a path. In transportation engineering, speed limits are set based on factors like road conditions, traffic volume, and geometric design. Higher speeds typically require wider curves with larger radii to ensure safe travel.

3. **Superelevation**: Superelevation, also known as banking or cant, is the inward tilt of a road or railway curve provided to counteract the effect of centrifugal force on vehicles traveling along the curve. It helps reduce the tendency of vehicles to overturn or skid outward during turns. Superelevation is typically expressed as a percentage.

**Superelevation (e)** is calculated using the formula:

e = {{v^2}}/{{g .r}}

Where: \( e \) = Superelevation (in %) \( v \) = Design speed of the curve (in m/s or ft/s) \( g \) = Acceleration due to gravity (approximately 9.81 m/s² or 32.2 ft/s²) \( r \) = Radius of the curve (in meters or feet)

To calculate the required superelevation for a given curve, you would rearrange the formula as follows:

\

[ e = \frac{{v^2}}/{{g \cdot r}} \] Let's say the design speed (\( v \)) is 30 m/s and the radius (\( r \)) of the curve is 100 meters. Using the formula: \[ e = \frac{{(30 \, \text{m/s})^2}}{{9.81 \, \text{m/s}^2 \cdot 100 \, \text{m}}} \] \[ e = \frac{{900 \, \text{m}^2/\text{s}^2}}{{981 \, \text{m}^2/\text{s}^2}} \] \[ e ≈ 0.917 \]

So, the required superelevation for this curve would be approximately 0.917%, meaning the outer edge of the curve would be elevated by that percentage compared to the inner edge.

Geometric design, considering factors such as radius, speed, and superelevation, plays a crucial role in ensuring safe and efficient transportation infrastructure. Here are ten benefits of geometric design:

1. **Safety**: Proper geometric design helps reduce the likelihood of accidents by providing appropriate curvature (radius) for the given speed limit. Safer curves are achieved by balancing the design speed with the superelevation.

2. **Vehicle Stability**: Superelevation ensures that vehicles maintain stability while negotiating curves, reducing the risk of rollovers or skidding.

3. **Comfort**: Well-designed curves with appropriate radii and superelevation provide a smoother ride for passengers, reducing discomfort and fatigue during travel.

4. **Increased Speed**: By optimizing curves with larger radii and suitable superelevation, vehicles can safely travel at higher speeds, improving travel time and efficiency.

5. **Capacity**: Proper geometric design allows for increased traffic capacity by facilitating smoother flow of vehicles through curves, reducing congestion and improving overall traffic flow.

6. **Reduced Maintenance Costs**: Roads and railways with well-designed geometry experience less wear and tear on vehicles and infrastructure, leading to lower maintenance costs over time.

7. **Fuel Efficiency**: Efficient geometric design reduces the need for braking and acceleration, resulting in improved fuel efficiency for vehicles traveling along the route.

8. **Accessibility**: Geometric design considerations enable the creation of transportation infrastructure that is accessible to a wider range of users, including pedestrians, cyclists, and people with disabilities

.

9. **Environmental Impact**: By optimizing geometric design, transportation planners can minimize environmental impacts such as soil erosion and habitat fragmentation, contributing to sustainable development.

10. **Emergency Response**: Well-designed roads and railways facilitate faster and safer emergency response by providing smooth curves that allow emergency vehicles to maintain higher speeds while maneuvering through the infrastructure.

These benefits demonstrate the importance of considering geometric design factors such as radius, speed, and superelevation in transportation infrastructure planning and design, ultimately leading to safer, more efficient, and sustainable transportation systems.

How To Earn From The Traqnsportation Geometric Design Calculation

:

Here are ten ways to earn money by leveraging skills related to transportation geometric design calculations:

1. **Consulting Services**: Offer consulting services to transportation agencies, engineering firms, or construction companies for designing and optimizing roadways, highways, and railways based on geometric design principles.

2. **Training and Workshops**: Conduct training sessions and workshops on transportation geometric design calculations for engineers, urban planners, and transportation professionals.

3. **Software Development**: Develop software tools and applications that assist engineers and planners in performing geometric design calculations for transportation infrastructure projects.

4. **Freelance Work**: Freelance as a transportation engineer specializing in geometric design calculations, offering your expertise on platforms like Upwork or Freelancer to clients worldwide.

5. **Educational Content Creation**: Create educational content such as online courses, ebooks, or video tutorials covering topics related to transportation geometric design calculations, and sell them through platforms like Udemy or Teachable.

6. **Research and Development**: Engage in research and development activities to improve existing geometric design calculation methods or develop new techniques, which can be licensed or sold to engineering firms or government agencies.

7. **Project Management**: Provide project management services for transportation infrastructure projects, overseeing the implementation of geometric design solutions and ensuring compliance with regulations and standards.

8. **Expert Witness Services**: Offer expert witness services in legal cases related to transportation accidents or disputes involving geometric design issues, providing expert testimony based on your expertise.

9. **Customized Solutions**: Develop customized geometric design solutions tailored to specific client needs or unique project requirements, offering a competitive advantage in the marketplace.

10. **Partnerships and Collaborations**: Partner with engineering firms, software developers, or government agencies to collaborate on transportation infrastructure projects or joint ventures, leveraging complementary expertise and resources.

By leveraging your expertise in transportation geometric design calculations, you can explore various opportunities to earn money and build a successful career in this specialized field.

Do YOU Want To Earn Money In Various Ways, Click The Link & Explore Your Field of Interest!!!

Hyperbola Calculator:Calculators for Students, Engineers & Researchers:Free Online Tool:

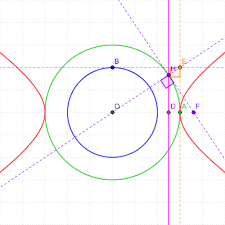
Defination: A hyperbola is a type of conic section, along with circles, ellipses, and parabolas. It's defined as the set of all points in a plane such that the absolute value of the difference of the distances from two fixed points (called the foci) is constant. In other words, for a hyperbola, the difference in distances from any point on the curve to the two foci remains constant.

Click the Translate button(see right) on this post to set your Own Language to understand more perfectly!!

Hyperbola Calculator

Coefficient 'a': Coefficient 'b':

Continue Definition:

A hyperbola is a type of conic section, along with circles, ellipses, and parabolas. It's defined as the set of all points in a plane such that the absolute value of the difference of the distances from two fixed points (called the foci) is constant. In other words, for a hyperbola, the difference in distances from any point on the curve to the two foci remains constant.

Equation of a Hyperbola:

The standard form of the equation of a hyperbola centered at the origin with its transverse axis along the x-axis is:

{

The standard form of the equation of a hyperbola centered at the origin with its transverse axis along the y-axis is:y^2}/{a^2} - {x^2}/{b^2} = 1

where:

(a) is the distance from the center to either vertex along the x-axis (semi-major axis),

(b) is the distance from the center to either endpoint of the conjugate axis along the y-axis (semi-minor axis).

The foci of the hyperbola are located along the x-axis at the points

( c, 0)), where (c = sqrt{a^2 + b^2+b}).

Properties of a Hyperbola:

1. **Center**: The center of the hyperbola is the point ((0, 0)\) if the hyperbola is centered at the origin.

2. **Vertices**: The vertices of the hyperbola are the points where it intersects its transverse axis.

3. **Foci**: The foci are the two fixed points inside the hyperbola.

4. **Asymptotes**: Hyperbolas have asymptotes, which are lines that the curve approaches but never intersects.

5. **Transverse Axis**: The axis passing through the vertices is called the transverse axis.

6. **Conjugate Axis**: The axis perpendicular to the transverse axis, passing through the center, is called the conjugate axis.

7. **Eccentricity**: The eccentricity of a hyperbola is the ratio of the distance from any point on the hyperbola to one of the foci over the distance from the same point to the corresponding directrix. It is denoted by (e) and is always greater than 1 for hyperbolas.

Examples of Hyperbolas:

1. **Satellite Orbits**: The paths of satellites around the Earth often follow hyperbolic trajectories.

2. **Conic Sections**: Hyperbolas can be found in nature as conic sections formed by intersecting a plane with a double cone.

3. **Optics**: Hyperbolic mirrors are used in certain types of telescopes and antennas to focus or reflect electromagnetic waves.

4. **Engineering**: Hyperbolic shapes are used in architecture and engineering, such as in the design of cooling towers or suspension bridges.

5. **Mathematics**: Hyperbolas are studied extensively in mathematics for their geometric properties and applications in various fields, including calculus and geometry.

How it is possible to EARN MONEY using Hyperbola Calculation in real life?????

Earning money directly through hyperbola calculations may be less common compared to other applications of mathematics. However, a strong understanding of hyperbolas and their properties can lead to opportunities in various fields where mathematical skills are valued. Here are some ways individuals can leverage hyperbola calculations to potentially earn money in real life:

1. **Engineering and Design Services**: Offer engineering or design services where hyperbolas are relevant, such as in the design of satellite trajectories, antennas, or architectural structures. A deep understanding of hyperbolas and their properties can be valuable in optimizing designs for efficiency and performance.

2. **Aerospace Industry**: Work in the aerospace industry, where hyperbolic trajectories are used in spacecraft navigation, orbit determination, and mission planning. Individuals with expertise in hyperbola calculations can contribute to the development and execution of space missions.

3. **Optics and Imaging Technologies**: Hyperbolas are used in optics for designing certain types of mirrors and lenses. Specialized knowledge of hyperbolas can be beneficial in industries involving optical systems, such as photography, astronomy, or laser technology.

4. **Math Tutoring and Education**: Offer tutoring services in mathematics, including geometry and conic sections. Hyperbolas are a fundamental topic in mathematics education, and individuals with expertise in this area can provide valuable instruction to students at various levels.

5. **Software Development**: Develop software tools or applications that utilize hyperbola calculations for specific purposes, such as simulation software for engineering or scientific research. These tools can be sold or licensed to companies and professionals in relevant industries.

6. **Consulting Services**: Provide consulting services to companies or research institutions that require expertise in hyperbola calculations for specific projects or applications. Consulting opportunities may arise in fields such as physics, geodesy, or telecommunications.

7. **Data Analysis and Modeling**: Use hyperbola equations and properties in mathematical modeling and data analysis for various applications, such as predicting trends, optimizing processes, or solving complex problems. Individuals with skills in mathematical modeling can find employment in industries like finance, economics, or environmental science.

8. **Research and Development**: Work in research and development roles where hyperbola calculations are essential for innovation and problem-solving. Industries such as defense, aerospace, and telecommunications often require research scientists and engineers with expertise in advanced mathematics.

While direct opportunities to earn money solely through hyperbola calculations may be limited, individuals with a strong mathematical background and expertise in hyperbolas can apply their skills in diverse fields where mathematical reasoning and problem-solving are valued.

Do YOU Want To Earn Money In Various Ways, Click The Link & Explore Your Field of Interest!!!