The On-Line Calculation fields are as i)Agriculture ii) Aircraft iii)General Math iv)Physics v)Chemistry vi)Chemical Engg. vii)Civil Engg. viii)Mechanical Engg. ix)EEC Engg. x) Fisheries Engg. xi) Poultry Engg. xii) Merine Engg. xiii) Nuclear Engg. xiv) Accounting and Finance. and many more. They assist Students, engineers, and researchers in analyzing and optimizing their regular work. It is the Blogpost for continuous use and I am requesting you to share as much as you can.
Donate for the Poorest Students
You can support for the poorest students. Copy the link in your browser & Donate as small as possible..
https://www.paypal.com/donate/?hosted_button_id=R3MNE48JU7KGL
Showing posts with label Geometry calculator. Show all posts
Showing posts with label Geometry calculator. Show all posts
Tuesday, 4 July 2023
Wednesday, 21 June 2023
Hyperbola Calculator:Calculators for Students, Engineers & Researchers:Free Online Tool:
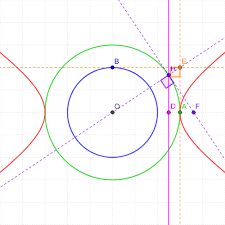
Defination: A hyperbola is a type of conic section, along with circles, ellipses, and parabolas. It's defined as the set of all points in a plane such that the absolute value of the difference of the distances from two fixed points (called the foci) is constant. In other words, for a hyperbola, the difference in distances from any point on the curve to the two foci remains constant.
Click the Translate button(see right) on this post to set your Own Language to understand more perfectly!!
Hyperbola Calculator
Continue Definition:
A hyperbola is a type of conic section, along with circles, ellipses, and parabolas. It's defined as the set of all points in a plane such that the absolute value of the difference of the distances from two fixed points (called the foci) is constant. In other words, for a hyperbola, the difference in distances from any point on the curve to the two foci remains constant.
Equation of a Hyperbola:
The standard form of the equation of a hyperbola centered at the origin with its transverse axis along the x-axis is:{
The standard form of the equation of a hyperbola centered at the origin with its transverse axis along the y-axis is:y^2}/{a^2} - {x^2}/{b^2} = 1
where:
(a) is the distance from the center to either vertex along the x-axis (semi-major axis),
(b) is the distance from the center to either endpoint of the conjugate axis along the y-axis (semi-minor axis).
The foci of the hyperbola are located along the x-axis at the points( c, 0)), where (c = sqrt{a^2 + b^2+b}).
Properties of a Hyperbola:
1. **Center**: The center of the hyperbola is the point ((0, 0)\) if the hyperbola is centered at the origin.
2. **Vertices**: The vertices of the hyperbola are the points where it intersects its transverse axis.
3. **Foci**: The foci are the two fixed points inside the hyperbola.
4. **Asymptotes**: Hyperbolas have asymptotes, which are lines that the curve approaches but never intersects.
5. **Transverse Axis**: The axis passing through the vertices is called the transverse axis.
6. **Conjugate Axis**: The axis perpendicular to the transverse axis, passing through the center, is called the conjugate axis.
7. **Eccentricity**: The eccentricity of a hyperbola is the ratio of the distance from any point on the hyperbola to one of the foci over the distance from the same point to the corresponding directrix. It is denoted by (e) and is always greater than 1 for hyperbolas.
Examples of Hyperbolas:
1. **Satellite Orbits**: The paths of satellites around the Earth often follow hyperbolic trajectories.
2. **Conic Sections**: Hyperbolas can be found in nature as conic sections formed by intersecting a plane with a double cone.
3. **Optics**: Hyperbolic mirrors are used in certain types of telescopes and antennas to focus or reflect electromagnetic waves.
4. **Engineering**: Hyperbolic shapes are used in architecture and engineering, such as in the design of cooling towers or suspension bridges.
5. **Mathematics**: Hyperbolas are studied extensively in mathematics for their geometric properties and applications in various fields, including calculus and geometry.
How it is possible to EARN MONEY using Hyperbola Calculation in real life?????
Earning money directly through hyperbola calculations may be less common compared to other applications of mathematics. However, a strong understanding of hyperbolas and their properties can lead to opportunities in various fields where mathematical skills are valued. Here are some ways individuals can leverage hyperbola calculations to potentially earn money in real life:
1. **Engineering and Design Services**: Offer engineering or design services where hyperbolas are relevant, such as in the design of satellite trajectories, antennas, or architectural structures. A deep understanding of hyperbolas and their properties can be valuable in optimizing designs for efficiency and performance.
2. **Aerospace Industry**: Work in the aerospace industry, where hyperbolic trajectories are used in spacecraft navigation, orbit determination, and mission planning. Individuals with expertise in hyperbola calculations can contribute to the development and execution of space missions.
3. **Optics and Imaging Technologies**: Hyperbolas are used in optics for designing certain types of mirrors and lenses. Specialized knowledge of hyperbolas can be beneficial in industries involving optical systems, such as photography, astronomy, or laser technology.
4. **Math Tutoring and Education**: Offer tutoring services in mathematics, including geometry and conic sections. Hyperbolas are a fundamental topic in mathematics education, and individuals with expertise in this area can provide valuable instruction to students at various levels.
5. **Software Development**: Develop software tools or applications that utilize hyperbola calculations for specific purposes, such as simulation software for engineering or scientific research. These tools can be sold or licensed to companies and professionals in relevant industries.
6. **Consulting Services**: Provide consulting services to companies or research institutions that require expertise in hyperbola calculations for specific projects or applications. Consulting opportunities may arise in fields such as physics, geodesy, or telecommunications.
7. **Data Analysis and Modeling**: Use hyperbola equations and properties in mathematical modeling and data analysis for various applications, such as predicting trends, optimizing processes, or solving complex problems. Individuals with skills in mathematical modeling can find employment in industries like finance, economics, or environmental science.
8. **Research and Development**: Work in research and development roles where hyperbola calculations are essential for innovation and problem-solving. Industries such as defense, aerospace, and telecommunications often require research scientists and engineers with expertise in advanced mathematics.
While direct opportunities to earn money solely through hyperbola calculations may be limited, individuals with a strong mathematical background and expertise in hyperbolas can apply their skills in diverse fields where mathematical reasoning and problem-solving are valued.
Do YOU Want To Earn Money In Various Ways, Click The Link & Explore Your Field of Interest!!!
Parabola Calculator:Calculators for Students, Engineers & Researchers:Free Online Tool:
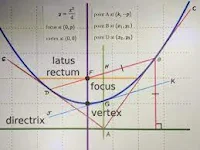
Definition: A parabola is a symmetric curve formed by the set of all points that are equidistant from a fixed line (the directrix) and a fixed point (the focus). Its equation in standard form depends on whether it opens upwards or downwards, or sideways.
Parabola Calculator
Continue Definition: Here's the standard form equation:
Vertical Parabola (opens upwards or downwards):
Equation: 𝑦=𝑎𝑥**2+𝑏𝑥+𝑐
where a, b, and c are constants, and 𝑎≠0
Horizontal Parabola (opens sideways):
Equation: 𝑥=𝑎𝑦**2+𝑏𝑦+𝑐
where a, b, and c are constants, and 𝑎≠0
For vertical parabolas: If 𝑎>0, the parabola opens upwards.
If a<0, the parabola opens downwards.
For horizontal parabolas: If a>0, the parabola opens to the right.
If a<0, the parabola opens to the left.
Understanding the basic properties of the coefficients
a, b, and c can help users grasp how the parabola is shaped and positioned.
Example:
One practical example of a parabola is the trajectory of a projectile under the influence of gravity. When an object is launched into the air at an angle, its path follows a parabolic shape due to the force of gravity acting on it.
Let's consider the example of a ball being thrown into the air. The path of the ball can be modeled by a vertical parabola. If we neglect air resistance, the equation of its trajectory can be expressed as:𝑦=𝑎𝑥**2+𝑏𝑥+𝑐
where : y represents the vertical position of the ball, x represents the horizontal position of the ball,
a is a constant determined by the initial velocity and angle of projection,
b is the horizontal velocity of the ball (which remains constant if air resistance is ignored)
c is the initial height from which the ball is thrown.
This parabolic trajectory shows the ball rising, reaching its maximum height, and then falling back to the ground. The shape of the trajectory is symmetric, with the highest point of the trajectory occurring at the vertex of the parabola.
This practical example demonstrates how parabolas are not just abstract mathematical concepts, but can be used to describe real-world phenomena, helping us understand and predict the behavior of objects in motion.
Usefullness of Parabola:
Satellite Dishes: The shape of satellite dishes is based on a parabolic curve. This design helps to collect and focus electromagnetic signals from satellites, ensuring efficient transmission of TV, internet, and other communication signals.
Flashlights and Headlights: Some flashlights and headlights utilize parabolic reflectors to focus and direct light beams. The parabolic shape helps in concentrating the light in a specific direction, enhancing brightness and visibility.
Solar Cookers: Parabolic solar cookers use the reflective properties of a parabolic mirror to concentrate sunlight onto a cooking vessel placed at the focal point. This method harnesses solar energy efficiently for cooking and other heating purposes.
Reflecting Telescopes: Many telescopes, including some of the most powerful ones in the world, use parabolic mirrors to gather and focus light from distant celestial objects. The parabolic shape allows for precise imaging and magnification.
Architectural Design: The graceful curve of a parabola is often incorporated into architectural designs to create aesthetically pleasing structures such as bridges, arches, and even buildings. The shape offers strength and stability while adding an elegant touch to the design.Projectile Motion: Parabolic trajectories are observed in projectile motion, such as the path of a thrown ball or a launched projectile. Understanding the mathematics of parabolas helps in predicting and analyzing the motion of objects in various scenarios, from sports to engineering.
Sound Reflection: In acoustics, parabolic shapes are utilized to reflect and focus sound waves, enhancing the quality and reach of sound in applications like megaphones and certain types of speakers.
Antenna Design: Parabolic antennas are commonly used in telecommunications and broadcasting for transmitting and receiving radio signals. The concave shape of the antenna helps to focus the signal in a specific direction, improving communication efficiency.
Water Fountains: Some water fountains feature parabolic shapes in their design, allowing water to be propelled upwards in an elegant arc. The curvature of the parabola contributes to the aesthetic appeal and functionality of the fountain.
Sporting Equipment: Parabolic shapes are incorporated into the design of sporting equipment such as ski ramps and snowboard halfpipes. These shapes optimize performance by providing smooth, predictable trajectories for athletes.
These applications illustrate the versatility and importance of parabolic curves in various fields, from technology and engineering to architecture and design.
HOW TO EARN MONEY UTLIZING PARABOLA CALCULATOR:Here are some ways you could monetize a Parabola Calculator:
Subscription Model: Offer premium features such as advanced graphing options, equation solving, and step-by-step solutions for a monthly or yearly subscription fee.
In-App Purchases: Provide additional tools or functionalities as in-app purchases, such as the ability to export graphs as high-resolution images or access to a library of pre-built parabola equations.
Ads: Integrate advertisements within the app, either as banners or interstitials, to generate revenue from user traffic. Freemium Model: Offer a basic version of the app for free with limited features, and then upsell users on a premium version with more advanced capabilities.
Affiliate Marketing: Partner with educational websites or online tutoring services and earn commissions for referring users to their platforms.
White Labeling: License your Parabola Calculator technology to other educational or math-focused apps, earning royalties or upfront fees for each integration.
Educational Resources: Create and sell educational materials such as ebooks, video courses, or interactive tutorials that complement the Parabola Calculator and help users deepen their understanding of parabolas and related concepts.
Consulting Services: Offer personalized consulting or tutoring services to individuals or educational institutions seeking assistance with parabola-related problems or math curriculum development.
Sponsorships: Seek sponsorships from math-related companies or educational institutions to promote their products or services within the app in exchange for financial support.
Crowdfunding: Launch a crowdfunding campaign to raise funds for further development of the Parabola Calculator or to introduce new features based on user feedback.
Each of these strategies has its pros and cons, so it's essential to consider your target audience, the value proposition of your app, and your long-term business goals when deciding on the best monetization approach.EARN MONEY USING PARABOLA CALCULATOR
Circle area and perimeter calculator:Calculators for Students, Engineers & Researchers:Free Online Tool:
Definition: This Circle Area and Perimeter Calculator helps you find the area and perimeter of a circle based on its radius.
Circle Calculator
Continue Definition: Here's a simple Circle Area and Perimeter Calculator along with some explanations:
Circle Area and Perimeter Calculator:
Equations: Area of a Circle (A):𝐴=𝜋×𝑟**2
A= represents the area of the circle.
π (pi) is a constant approximately equal to 3.14159.
r is the radius of the circle.
Perimeter of a Circle (P):𝑃=2×𝜋×𝑟
P represents the perimeter of the circle.
π (pi) is a constant approximately equal to 3.14159.
r is the radius of the circle.
Description:
This Circle Area and Perimeter Calculator helps you find the area and perimeter of a circle based on its radius.
Here's how to use it:
Input: Enter the radius of the circle into the designated field.
Calculate: Click the "Calculate" button.
Output: The calculator will display both the area and perimeter of the circle based on the provided radius.
Example:
Let's say you have a circle with a radius of 5 units.
Area: Using the formula,
𝐴=𝜋×𝑟**2
where,𝑟=5
𝐴=𝜋×5**2=𝜋×25≈78.54square units
Perimeter: Using the formula,
𝑃=2×𝜋×𝑟
where
𝑟=5 units:
𝑃=2×𝜋×5≈31.42 units
So, for a circle with a radius of 5 units, the area is approximately 78.54 square units, and the perimeter is approximately 31.42 units.
Benefits:
User-Friendly: This calculator is easy to use and understand, making it suitable for users of all levels.
Quick Results: By simply inputting the radius, users can obtain the area and perimeter of a circle in no time.
Educational: The accompanying equations and descriptions can help users understand the mathematical concepts behind the calculations.
Usefulness of Circle area & Perimeter Calculation:
Home Décor: Circular rugs, mirrors, and wall clocks are popular decorative items. Knowing the area helps in selecting the right size for a space, while the perimeter might be useful for choosing suitable framing or hanging options.
Fashion Design: Circular patterns, such as ruffles, flounces, or circular skirts, are common in fashion. Understanding the area and perimeter assists designers in fabric cutting, pattern drafting, and creating garment silhouettes.
DIY Projects: Whether you're crafting a circular table, a clock face, or a decorative wreath, knowing the area and perimeter helps you plan and execute your DIY projects more efficiently.
Vehicle Maintenance: Circular components like tires and brake rotors are essential parts of vehicles. Calculating the area and perimeter aids in determining tire sizes, brake pad requirements, and maintenance schedules.
Medical Field: Circular imaging techniques, such as MRIs and CT scans, are crucial for diagnosing various medical conditions. Understanding the area and perimeter helps medical professionals analyze and interpret these images accurately.
Environmental Science: Circular plots are often used in ecological studies to measure plant distribution, biodiversity, or pollution levels. Calculating their area and perimeter assists researchers in collecting and analyzing field data.
Navigation: Circular navigation tools, like compasses and astrolabes, have been historically used for orientation and celestial navigation. Understanding the principles behind their design involves knowledge of circle geometry.
Finance and Investments: Circular concepts, such as compound interest and annuities, are fundamental in financial calculations. Knowing how to calculate the area and perimeter of financial models aids in making informed investment decisions.
HOW TO EARN MONEY USING CIRCLE AREA & PERIMETER CALCULATION???
Here are several practical ways individuals can earn money by leveraging their knowledge of circle area and perimeter calculations:
1. **Landscaping and Gardening Services:** Offer landscaping and gardening services where you design and maintain circular flower beds or lawns. Knowledge of circle area helps in planning the layout and estimating materials like plants, mulch, or paving stones needed for the project. Calculate the area of circular lawns or garden beds accurately to provide clients with precise cost estimates.
2. **Swimming Pool Installation and Maintenance:** If you're in the business of installing or maintaining swimming pools, understanding circle area is crucial. Pools are often circular or have circular sections. Calculate the surface area of circular pools to estimate the amount of water needed to fill them or the cost of materials for lining or tiling.
3. **Art and Craft Projects:** Create and sell custom-made circular artwork, such as mandala paintings or stained glass designs. Knowledge of circle area and perimeter helps in designing and framing these artworks. Offer workshops or online courses teaching people how to create their own circular artwork using mathematical principles.
4.**Construction and Architecture:** Architects and builders often design structures with circular elements like domes, arches, or circular windows. Understanding circle area and perimeter is essential for accurate measurement and construction. Offer consulting services to construction companies or homeowners looking to incorporate circular features into their buildings or renovations.
5. **Fabrication and Manufacturing:** If you're involved in fabrication or manufacturing, knowing circle area and perimeter is useful for creating circular components or products. Fabricate circular metal or plastic parts for machinery, equipment, or consumer products based on precise measurements and calculations.
6. **Event Planning and Decoration:** Plan and decorate events such as weddings, parties, or corporate functions where circular elements like tables, stages, or dance floors are common. Calculate the area of circular spaces to determine the number of guests a venue can accommodate or to plan the layout of seating arrangements.
7. **Teaching and Tutoring:** Offer tutoring services in mathematics, focusing on geometry and practical applications like circle area and perimeter calculations. Create educational materials, such as worksheets or online courses, to help students understand and apply mathematical concepts in real-life scenarios.
8. **Real Estate and Property Development:** - Real estate agents and property developers can use circle area calculations to assess the size and value of circular parcels of land or to design circular buildings or structures. - Provide consulting services to clients interested in purchasing or developing properties with circular features.
By applying their knowledge of circle area and perimeter calculations in these practical ways, individuals can earn money while also providing valuable services to their clients or customers.1000's of ways to EARN MONEY, CLICK & EXPLORE
Rhombus Calculator:Calculators for Students, Engineers & Researchers:Free Online Tool:
Definition: A rhombus is a four-sided flat shape where all four sides are equal in length, the diagonals of a rhombus bisect each other at right angles, creating four right triangles. Diagonal length (d1 or d2) = s√(2 + 2 cos(θ)). s is the side length of the rhombus. θ is the angle between two adjacent sides of the rhombus (opposite angles are equal in a rhombus). Two adjacent angels of a rhombus is equal to 180 degree.
Click the Translate button(see right) on this post to set your Own Language to understand more perfectly!!
Rhombus Calculator
Continue Definition:
A rhombus is a four-sided flat shape where all four sides are equal in length.
Rhombus Area:
The area of a rhombus can be calculated in two ways:
Using the base (b) and height (h):
Area = b * h
(This is similar to how you calculate the area of a rectangle.)
Using the diagonals (d1 and d2):
Area = (d1 * d2) / 2
(This formula takes advantage of the fact that the diagonals of a rhombus bisect each other at right angles, creating four right triangles.)
Diagonal Length: There are two diagonals in a rhombus, and they are perpendicular to each other. We don't have a specific formula to directly calculate one diagonal based on the other, but we can use the side length (s) of the rhombus to find them both.
Here's the formula for the diagonals:
Diagonal length (d1 or d2) = s√(2 + 2 cos(θ))
where:
s is the side length of the rhombus
θ is the angle between two adjacent sides of the rhombus (all four angles are equal in a rhombus)
Example 1: Area using base and height
Imagine a rhombus with a base of 6 cm and a height of 4 cm.
Area = b * h = 6 cm * 4 cm = 24 cm²
Example 2: Area using diagonals
Let's say another rhombus has diagonals measuring 8 cm and 10 cm.
Area = (d1 * d2) / 2 = (8 cm * 10 cm) / 2 = 40 cm²
Example 3: Diagonal Length
Consider a rhombus with a side length of 5 cm and an angle of 60 degrees between two adjacent sides (θ = 60°).
Diagonal length = s√(2 + 2 cos(θ)) = 5 cm√(2 + 2 cos(60°)) ≈ 8.66 cm (We can use a calculator to approximate the value.)
How it is possible to EARN MONEY using Rhombus Calculation???
Rhombus calculations, which involve finding the area, perimeter, or other properties of a rhombus, may not directly translate into standalone money-making ventures. However, understanding geometry and mathematical concepts like those used in rhombus calculations can be applied in various real-life situations, some of which may potentially lead to earning money.
Here are a few examples:
1. **Engineering and Architecture**: Professionals in these fields often use geometric concepts, including rhombus calculations, when designing structures, layouts, or mechanical components. While the direct application may not involve rhombuses specifically, a strong understanding of geometry is essential for success in these professions.
2. **Graphics and Design**: Graphic designers, artists, and illustrators may use geometric shapes, including rhombuses, in their work. While the direct application of rhombus calculations might be limited, the ability to create visually appealing designs can lead to freelance opportunities or employment in various industries.
3. **Education**: If you have a deep understanding of rhombus calculations and mathematics in general, you could potentially earn money by tutoring or teaching others. There's always a demand for qualified math tutors, especially for students struggling with geometry concepts.
4. **Software Development**: Knowledge of geometry, including rhombus calculations, can be useful in fields like computer graphics or game development. While not directly related to rhombuses, the ability to manipulate geometric shapes and understand spatial relationships is valuable in creating software applications.
5. **Data Analysis and Statistics**: While it may seem unrelated at first, a strong foundation in mathematics, including geometry, can be beneficial in fields like data analysis and statistics. Many industries rely on data-driven decision-making, and individuals with strong analytical skills are often in demand.
6. **Problem Solving and Consulting**: Some companies may hire individuals with strong mathematical skills, including geometry, to help solve complex problems or optimize processes. While the specific application of rhombus calculations may be rare, the problem-solving abilities gained from studying geometry can be valuable in various contexts.
While directly earning money through rhombus calculations might be limited, the skills and knowledge gained from studying geometry can open doors to various opportunities in a wide range of industries.
Do YOU Want To Earn Money In Various Ways, Click The Link & Explore Your Field of Interest!!!
Parallelogram Calculator:Calculators for Students, Engineers & Researchers:Free Online Tool:
Definition: A parallelogram is a four-sided flat shape where opposite sides are parallel and equal in length.
Click the Translate button(see right) on this post to set your Own Language to understand more perfectly!!Parallelogram Calculator Parallelogram Calculator
Continue Definition:A parallelogram is a four-sided flat shape where opposite sides are parallel and equal in length. Here are some of its properties along with equations and examples for better understanding:Properties of a ParallelogramOpposite sides Opposite sides are parallel and congruent (equal in length).A parallelogram with sides measuring 5 cm and 7 cm will have two sides of 5 cm each and two sides of 7 cm each.Consecutive angles: Consecutive interior angles are supplementary (add up to 180 degrees).∠A + ∠B = 180°∠B + ∠C = 180°∠C + ∠D = 180°∠D + ∠A = 180°Let's consider a parallelogram ABCD. If ∠A = 60°, then ∠B = 120° , If ∠A = 120°. then ∠B = 60° ,Opposite angles Opposite interior angles are congruent (equal). ∠A = ∠C, and. ∠B = ∠D.In parallelogram ABCD, if ∠A = 60°, then ∠C = 60° (opposite angles).Diagonals: Diagonals bisect each other (cut each other in half at a point).Imagine a parallelogram ABCD. Diagonals AC and BD intersect at point E. This implies that AE = EC and BE = ED.Area and Perimeter of a ParallelogramThe area and perimeter of a parallelogram can be calculated using the following formulas:Area: A = base * height, where base is the length of the base and height is the perpendicular distance from the base to the opposite side.Perimeter: P = 2(side1 + side2), where side1 and side2 are the lengths of any two adjacent sides of the parallelogram.For example, if a parallelogram has a base of 10 cm and a height of 5 cm, its area would be 50 cm² (10 cm * 5 cm). If another parallelogram has adjacent sides of 8 cm and 12 cm, its perimeter would be 40 cm (2 * (8 cm + 12 cm)).How it is possiable to EARN MONEY using Parallelogram Calculator in the real life???Usefulness of Parallelogram in our daily life:Parallelograms are geometric shapes with several properties that make them useful in various real-life applications. Some of the key uses and properties of parallelograms include:1. **Area Calculation**: Parallelograms can be used to calculate the area of various objects and surfaces, such as fields, rooms, or parcels of land.2. **Structural Design**: Engineers and architects use parallelograms in designing structures such as bridges, buildings, and frameworks due to their stability and uniform distribution of forces.3. **Packaging and Design**: Parallelograms are used in designing packaging materials and layouts for efficient use of space and material.4. **Mechanical Engineering**: Parallelograms are utilized in designing mechanical components and systems, such as linkages and conveyor belts.5. **Mathematical Modeling**: Parallelograms are often used in mathematical modeling to represent various real-world phenomena, such as vectors and force diagrams.6. **Surveying and Mapping**: Surveyors use parallelograms to measure and calculate distances, angles, and areas in land surveying and cartography.7. **Computer Graphics**: Parallelograms are used in computer graphics for rendering objects, creating textures, and simulating physical phenomena.8. **Interior Design**: Interior designers use parallelograms to plan layouts of rooms, furniture arrangements, and decorative elements for optimal use of space and aesthetics.9. **Manufacturing and Production**: Parallelograms are used in manufacturing processes for cutting materials, forming shapes, and optimizing production layouts.10. **Education and Learning**: Parallelograms are an essential topic in mathematics education, providing students with foundational knowledge in geometry and problem-solving skills.Now, here are 10 key points to earn money in real life using a parallelogram calculator:1. **Land Surveying**: Offer services to land surveyors by using a parallelogram calculator to accurately measure and calculate land areas.2. **Architectural Design**: Provide architectural firms with assistance in designing structures by calculating areas, angles, and dimensions using parallelogram properties.3. **Graphic Design**: Offer graphic design services specializing in packaging design, utilizing parallelogram calculations for efficient use of space and material.4. **Mechanical Engineering**: Provide consulting services to mechanical engineering firms, assisting in designing components and systems using parallelogram calculations.5. **Math Tutoring**: Offer tutoring services in mathematics, focusing on geometry and providing students with tools and techniques to solve parallelogram-related problems.6. **Online Courses**: Create and sell online courses or tutorials on platforms like Udemy or Coursera, teaching others how to use parallelogram calculations in various real-life scenarios.7. **App Development**: Develop a mobile or web-based app that serves as a parallelogram calculator, catering to professionals in fields such as engineering, architecture, and design.8. **Consulting**: Start a consulting business offering expertise in utilizing parallelogram calculations for optimizing processes and solving complex problems in various industries.9. **Manufacturing Optimization**: Offer services to manufacturing companies to optimize production processes and layouts using parallelogram calculations for material efficiency.10. **Freelance Work**: Offer freelance services on platforms like Upwork or Fiverr, providing customized parallelogram calculations and solutions to clients from diverse industries.Do YOU Want To Earn Money In Various Ways, Click The Link & Explore Your Field of Interest!!!
Triangle area and perimeter Calculator:Calculators for Students, Engineers & Researchers:Free Online Tool:
Definition: This Triangle Area and Perimeter Calculator helps you find the area and perimeter of a triangle based on its side lengths and height.
Click Translate button on this post( see right) to set your Own Language to understand more perfectly!!
Triangle Calculator
Continue Definition:
Here's a Triangle Area and Perimeter Calculator along with explanations:
Triangle Area and Perimeter Calculator
Equations:
Area of a Triangle (A):𝐴=(1/2)×𝑏×ℎ
A, represents the area of the triangle.
b, is the base of the triangle.
h, is the height of the triangle perpendicular to the base.
Perimeter of a Triangle (P):𝑃=𝑎+𝑏+𝑐
P, represents the perimeter of the triangle. a, b, and 𝑐 are the lengths of the three sides of the triangle.
Description:
This Triangle Area and Perimeter Calculator helps you find the area and perimeter of a triangle based on its side lengths and height.
Here's how to use it:
Input: Enter the lengths of the three sides of the triangle and the height perpendicular to the base into the designated fields.
Calculate: Click the "Calculate" button.
Output: The calculator will display both the area and perimeter of the triangle based on the provided measurements.
Example: Let's say you have a triangle with side lengths a=5, b=8, and c=10 units, and a height h=6 units.
Area: Using the formula, 𝐴=(1/2)×𝑏×ℎ
where b=8 and h=6: 𝐴=24 square units
Perimeter: Using the formula, P=a+b+c, where a=5, b=8, and c=10:P=5+8+10=23units
So, for a triangle with side lengths a=5, b=8, and c=10 units, and a height h=6 units, the area is 24 square units, and the perimeter is 23 units.
Benefits:
User-Friendly: This calculator is easy to use and understand, making it suitable for users of all levels.
Versatile: Users can input different combinations of side lengths and heights to calculate the area and perimeter of various types of triangles.
Educational: The accompanying equations and descriptions can help users understand the mathematical concepts behind the calculations.
Feel free to integrate this calculator into your application or website to provide a convenient tool for your users!
How it is possible to earn money using triangle area & perimeter calculation??
Here are several practical ways individuals can earn money by applying their knowledge of triangle area and perimeter calculations:
Construction and Carpentry:
Offer services in construction or carpentry where knowledge of triangle geometry is essential for tasks like framing roofs, building stairs, or constructing triangular structures.
Calculate the area of triangular spaces to estimate the amount of materials needed for projects like roofing or flooring. Interior Design and Decoration:
Provide interior design services where understanding triangle geometry helps in arranging furniture, designing floor plans, or creating visually appealing layouts.
Offer custom-made triangular shelving units, decorative wall panels, or furniture pieces designed using geometric principles.
Surveying and Landscaping:
Work as a surveyor or landscaper where knowledge of triangle geometry is crucial for measuring land plots, planning garden layouts, or designing pathways and irrigation systems.
Calculate the area of triangular sections in landscapes to estimate the quantity of soil, plants, or paving materials required for landscaping projects.
Graphic Design and Illustration:
Create and sell geometric-themed artwork, such as posters, prints, or digital illustrations, incorporating triangles and other geometric shapes.
Offer design services for logos, branding, or marketing materials using triangle motifs to convey modernity, stability, or creativity.
Education and Tutoring:
Provide tutoring services in mathematics, focusing on geometry and practical applications like triangle area and perimeter calculations.
Develop educational resources, such as worksheets, lesson plans, or online courses, to help students understand and apply geometric concepts in real-life situations.
Architecture and Urban Planning:
Work as an architect or urban planner where knowledge of triangle geometry is essential for designing buildings, city layouts, or transportation networks.
Offer consulting services to developers or municipalities on projects involving triangular parcels of land, intersections, or public spaces.
Event Planning and Management:
Plan and manage events such as weddings, conferences, or festivals where understanding triangle geometry helps in designing seating arrangements, stage layouts, or exhibition spaces.
Calculate the area of triangular tents, marquees, or event venues to determine capacity and pricing for rental purposes.
Manufacturing and Fabrication:
Work in manufacturing or fabrication industries where knowledge of triangle geometry is necessary for creating triangular components or products.
Fabricate custom-made triangular structures, architectural features, or industrial parts based on precise measurements and calculations.
By applying their knowledge of triangle area and perimeter calculations in these practical ways, individuals can earn money while also providing valuable services to their clients or customers.
Do YOU Want To Earn Money In Various Ways, Click The Link & Explore Your Field of Interest!!!
icosa Calculator:Calculators for Students, Engineers & Researchers:Free Online Tool:
Definition: An icosahedron geometry calculator helps you determine the surface area and volume of a regular icosahedron, a Platonic solid with 20 equilateral triangle faces.
Click the Translate button(see right) on this post to set your Own Language to understand more perfectly!!Icosa Calculator Icosa Calculator
Cotinue Definition:Icosahedron Geometry CalculatorAn icosahedron geometry calculator helps you determine the surface area and volume of a regular icosahedron, a Platonic solid with 20 equilateral triangle faces.Here's the breakdown with formulas and an example:How to calculate Interior angle of a polygon:Interior Angle (θ): The interior angle of a regular polygon (where all sides and angles are equal) can be calculated by dividing the sum of all internal angles by the number of sides.Equation: 𝜃={(𝑛−2)×180°/𝑛}n is the number of sides.Example: For a regular polygon, 𝑛=20so the interior angle would be =162°.Formulas:Surface Area:Surface Area (SA) = 5 * √3 * a^2where:a = edge length of the icosahedron (all edges are equal in a regular icosahedron)√3 (square root of 3) is a mathematical constant with a value of approximately 1.732Volume:Volume (V) = (5 * (3 + √5)) * a^3 / 12where:a = edge length of the icosahedron√5 (square root of 5) is another mathematical constant with a value of approximately 2.236Example:Imagine you have a beautiful, handcrafted icosahedron with an edge length of 5 centimeters (cm). You want to know its surface area and volume to calculate the amount of paint needed to coat it entirely.Surface Area Calculation:Plug the edge length (a) into the formula:SA = 5 * √3 * (5 cm)^2Simplify the equation:SA = 5 * √3 * 25 cm^2 ≈ 65.35 cm^2 (using a calculator for √3)Therefore, the total surface area of the icosahedron is approximately 65.35 square centimeters.Volume Calculation:Plug the edge length (a) into the formula:V = (5 * (3 + √5)) * (5 cm)^3 / 12Simplify the equation (using a calculator for √5):V ≈ (5 * (3 + 2.236)) * 125 cm^3 / 12 ≈ 309.4 cm^3Therefore, the volume of the icosahedron is approximately 309.4 cubic centimeters.How to earn money in our real life with the application of icosahedron calculatorWhile an icosahedron calculator itself isn't a direct way to make money, it can be a valuable tool in a few strategies to generate income related to fields that utilize icosahedra. Here are some possibilities:1. Educational Content Creation:Target Audience: Students, artists, or designers interested in 3D geometry, particularly Platonic solids.Content: Develop engaging content explaining the icosahedron's properties, its applications in various fields, and how to use the icosahedron calculator effectively.This could include:Blog posts or articles explaining the formulas and their applications.Video tutorials demonstrating how to use the calculator and interpret the results.Interactive web applications incorporating the calculator with visualizations of the icosahedron.Monetization:Implement advertising on your website or channel.Offer premium content like downloadable 3D models or in-depth guides on specific icosahedron applications for a fee.Partner with educational platforms to provide your content as a learning resource.2. 3D Printing Services:Target Audience: People who need custom-made icosahedron models for various purposes (educational models, art projects, design prototypes).Service: Offer 3D printing services alongside the icosahedron calculator.The calculator allows customers to determine the exact size (based on edge length) needed for their project.You can create 3D printable models of icosahedrons in various sizes and materials.Monetization: Charge a fee for the 3D printing service based on the model size, material, and complexity.3. Custom Art & Design Projects:Target Audience: Artists, designers, or architects who incorporate icosahedrons in their work.Service: Offer custom design or fabrication services using your knowledge of icosahedron geometry and the calculator.This could involve creating decorative icosahedron sculptures, designing furniture pieces inspired by the shape, or even developing architectural elements using icosahedral structures.Monetization: Charge a project fee based on the complexity of the design, materials used, and fabrication time.4. Educational Workshops & Tutorials:Target Audience: Teachers, students, or hobbyists interested in learning more about 3D geometry and Platonic solids.Service: Conduct workshops or online tutorials focused on icosahedra.These sessions can involve using the icosahedron calculator to explore the relationships between edge length, surface area, and volume.You can incorporate hands-on activities like building paper models of icosahedrons.Monetization: Charge a registration fee for workshops or offer tiered pricing for online tutorials based on the level of detail and resources provided.Remember: The key is to leverage your knowledge of the icosahedron calculator to provide valuable solutions, resources, or educational content to audiences who might find the icosahedron's properties and applications interesting or beneficial.Do YOU Want To Earn Money In Various Ways, Click The Link & Explore Your Field of Interest!!!
Dodecagon Calculator:Calculators for Students, Engineers & Researchers:Free Online Tool:
Definition: If by "12 side enclosed area" you meant a Dodecagon, which is a 12-sided polygon, then a calculator could be designed for this specific shape.The area of a Dodecagon can be calculated by dividing it into smaller shapes like triangles or quadrilaterals and summing their areas. There's no single universal formula for a decagon's area as it depends on how the decagon is divided.
Sum of interior angles = (n - 2) x 180°, where n is the number of sides in the polygon. For a nonagon (n = 12):Sum of interior angles = (12 - 2) x 180° = 10 x 180° = 1800°. This formula tells you that all the interior angles of a nonagon add up to 1880 degrees. However, it doesn't tell you the measure of each individual angle.<2b>Regular Nonagon: If the Do0ecagon is a regular Dodecagon (all sides and angles equal), then each interior angle can be found using this formula:Each interior angle = Sum of interior angles / number of sides=1800/12=150 degree.
Click the Translate button(see right) on this post to set your Own Language to understand more perfectly!!
Dodecagon Calculator
Continue Definition:
A 12-sided enclosed area calculator isn't a standard tool because a specific geometric shape with 12 sides doesn't have a universally recognized name.
However, there are two possible interpretations:
Dodecagon Calculator: If by "12 side enclosed area" you meant a Dodecagon , which is a 12-sided polygon, then a calculator could be designed for this specific shape.
Here's what you'd need:
Formula: The area of Dodecagon a can be calculated by dividing it into smaller shapes like triangles or quadrilaterals and summing their areas. There's no single universal formula for a Dodecagon's area as it depends on how the Dodecagon is divided.
Example: Let's say you have a Dodecagon where all sides are equal (regular dedecagon) and you can divide it into 12 congruent triangles by drawing lines from each vertex to the center. If each side length is s, each triangle will have a base of s and a height reaching the center which can be calculated using trigonometry (depending on the available information about angles). By summing the area of all 12 triangles (1/2 * base * height), you'd get the total area of the decagon.
General Polygon Calculator: A more general approach is to use a polygon area calculator. This type of calculator can handle any polygon, including a 12-sided one. It typically requires you to input the side lengths and some additional information depending on the specific polygon type (e.g., angles for a regular polygon).
Here's a general formula for a polygon (not specific to nine sides):
Shoelace Theorem: This formula uses the signed shoelace algorithm to calculate the area of any polygon. It involves multiplying subsequent side lengths with the change in y-coordinates and vice versa, then summing the products and dividing by 2.
Important Note: Using the shoelace theorem requires the polygon's vertices' coordinates (x, y positions).
In conclusion: While there isn't a specific "12-sided enclosed area calculator," the concepts of regular decagons and polygon area calculators can help you determine the enclosed area of a 12-sided shape. The approach depends on whether you have a specific Dodecagon (with known side lengths or angles) or a general 12-sided polygon with available vertexcoordinates.
How to measure interior angle of any polygon:
Angle Measurement Equation:
The sum of the interior angles of any polygon can be calculated using the following formula:
Sum of interior angles = (n - 2) x 180°
where n is the number of sides in the polygon.
For a nonagon (n = 12):Sum of interior angles = (12 - 2) x 180° = 10 x 180° = 1800°
This formula tells you that all the interior angles of a nonagon add up to 1800 degrees. However, it doesn't tell you the measure of each individual angle.
Regular Decagon:
If the decagon is a regular decagon (all sides and angles equal), then each interior angle can be found using this formula:
Each interior angle = Sum of interior angles / number of sides
Each interior angle = 1800° / 11 = 150°
Therefore, in a regular hendecagon , each interior angle measures 150 degrees.
Irregular hendecagon:
For an irregular Dodecagon (sides and angles not all equal), you cannot determine the measure of each individual angle using a single formula. You would need additional information about the specific Dodecagon, such as the measure of some of its angles or side lengths, to calculate the remaining angles using geometric principles.
How it is possible to EARN MONEY using Dodecagon Calculation in our real life???
A 12-sided enclosed area calculation itself isn't a direct way to earn money. However, the ability to calculate areas can be valuable in several real-world scenarios that could lead to earning income. Here are some possibilities:
Construction and Handyman Services: Calculating areas is crucial in construction and handyman work. If you can accurately calculate floor space, wall areas, or roofing materials needed, you could offer services like:
Estimating materials and costs for renovation projects.
Helping people plan furniture placement in their homes.
Creating floor plans for small additions.
Landscaping and Gardening: Landscapers and gardeners often need to calculate areas for tasks like:
Determining the amount of mulch, sod, or gravel needed for a project.
Calculating the size of a patio or walkway.
Designing irrigation systems.
Interior Design: Interior designers use area calculations for:
Determining furniture layout and spacing.
Calculating carpet or flooring needs.
Creating space plans for clients.
Real Estate: Real estate agents and appraisers use area calculations to:
Determine the square footage of a property.
Compare property size to similar listings.
Estimate property value based on size.
Earning through Online Platforms:
You could leverage your area calculation skills on online platforms like:
Freelancing Websites: Offer your services as a virtual assistant for tasks requiring area calculations.
Tutoring Platforms: Tutor students in geometry or math, focusing on area calculations.
Additional Tips:
While a 11-sided shape might not be common, being comfortable with various polygon shapes and area formulas is beneficial.
Consider learning basic drafting software that often includes area calculation tools.
Combining your area calculation skills with additional knowledge (construction materials, plant needs, etc.) can increase your earning potential.
The key is to identify how your ability to calculate areas translates into a valuable service for people in various industries.
Do YOU Want To Earn Money In Various Ways, Click The Link & Explore Your Field of Interest!!!
Decagon Calculator:Calculators for Students, Engineers & Researchers:Free Online Tool:
Definition: If by "Ten side enclosed area" you meant a decagon, which is a ten-sided polygon, then a calculator could be designed for this specific shape.The area of a decagon can be calculated by dividing it into smaller shapes like triangles or quadrilaterals and summing their areas. There's no single universal formula for a decagon's area as it depends on how the decagon is divided.
Sum of interior angles = (n - 2) x 180°, where n is the number of sides in the polygon. For a nonagon (n = 10):Sum of interior angles = (10 - 2) x 180° = 8 x 180° = 1440°. This formula tells you that all the interior angles of a nonagon add up to 1440 degrees. However, it doesn't tell you the measure of each individual angle.Regular Nonagon: If the nonagon is a regular nonagon (all sides and angles equal), then each interior angle can be found using this formula:Each interior angle = Sum of interior angles / number of sides=1440/10=144 degree.
Click the Translate button(see right) on this post to set your Own Language to understand more perfectly!!
Decagon Calculator
Continue Definition:
A Ten-sided enclosed area calculator isn't a standard tool because a specific geometric shape with ten sides doesn't have a universally recognized name.
However, there are two possible interpretations:
Decagon Calculator: If by "ten side enclosed area" you meant a decagon, which is a ten-sided polygon, then a calculator could be designed for this specific shape.
Here's what you'd need:
Formula: The area of a decagon can be calculated by dividing it into smaller shapes like triangles or quadrilaterals and summing their areas. There's no single universal formula for a decagon's area as it depends on how the decagon is divided.
Example: Let's say you have a decagon where all sides are equal (regular decagon) and you can divide it into nine congruent triangles by drawing lines from each vertex to the center. If each side length is s, each triangle will have a base of s and a height reaching the center which can be calculated using trigonometry (depending on the available information about angles). By summing the area of all Ten triangles (1/2 * base * height), you'd get the total area of the decagon.
General Polygon Calculator: A more general approach is to use a polygon area calculator. This type of calculator can handle any polygon, including a nine-sided one. It typically requires you to input the side lengths and some additional information depending on the specific polygon type (e.g., angles for a regular polygon).
Here's a general formula for a polygon (not specific to nine sides):
Shoelace Theorem: This formula uses the signed shoelace algorithm to calculate the area of any polygon. It involves multiplying subsequent side lengths with the change in y-coordinates and vice versa, then summing the products and dividing by 2.
Important Note: Using the shoelace theorem requires the polygon's vertices' coordinates (x, y positions).
In conclusion: While there isn't a specific "Ten-sided enclosed area calculator," the concepts of regular decagons and polygon area calculators can help you determine the enclosed area of a ten-sided shape. The approach depends on whether you have a specific decagon (with known side lengths or angles) or a general ten-sided polygon with available vertex coordinates.
How to measure interior angle of any polygon:
Angle Measurement Equation:
The sum of the interior angles of any polygon can be calculated using the following formula:
Sum of interior angles = (n - 2) x 180°
where n is the number of sides in the polygon.
For a nonagon (n = 10):Sum of interior angles = (10 - 2) x 180° = 7 x 180° = 1440°
This formula tells you that all the interior angles of a nonagon add up to 1440 degrees. However, it doesn't tell you the measure of each individual angle.
Regular Decagon:
If the decagon is a regular decagon (all sides and angles equal), then each interior angle can be found using this formula:
Each interior angle = Sum of interior angles / number of sides
Each interior angle = 1440° / 10 = 1440°
Therefore, in a regular nonagon, each interior angle measures 144 degrees.
Irregular Decagon:
For an irregular Decagon (sides and angles not all equal), you cannot determine the measure of each individual angle using a single formula. You would need additional information about the specific decagon, such as the measure of some of its angles or side lengths, to calculate the remaining angles using geometric principles.
How it is possible to EARN MONEY using Decogen Calculation in our real life???
A Ten-sided enclosed area calculation itself isn't a direct way to earn money. However, the ability to calculate areas can be valuable in several real-world scenarios that could lead to earning income. Here are some possibilities:
Construction and Handyman Services: Calculating areas is crucial in construction and handyman work. If you can accurately calculate floor space, wall areas, or roofing materials needed, you could offer services like:
Estimating materials and costs for renovation projects.
Helping people plan furniture placement in their homes.
Creating floor plans for small additions.
Landscaping and Gardening: Landscapers and gardeners often need to calculate areas for tasks like:
Determining the amount of mulch, sod, or gravel needed for a project.
Calculating the size of a patio or walkway.
Designing irrigation systems.
Interior Design: Interior designers use area calculations for:
Determining furniture layout and spacing.
Calculating carpet or flooring needs.
Creating space plans for clients.
Real Estate: Real estate agents and appraisers use area calculations to:
Determine the square footage of a property.
Compare property size to similar listings.
Estimate property value based on size.
Earning through Online Platforms:
You could leverage your area calculation skills on online platforms like:
Freelancing Websites: Offer your services as a virtual assistant for tasks requiring area calculations.
Tutoring Platforms: Tutor students in geometry or math, focusing on area calculations.
Additional Tips:
While a Ten-sided shape might not be common, being comfortable with various polygon shapes and area formulas is beneficial.
Consider learning basic drafting software that often includes area calculation tools.
Combining your area calculation skills with additional knowledge (construction materials, plant needs, etc.) can increase your earning potential.
The key is to identify how your ability to calculate areas translates into a valuable service for people in various industries.
Do YOU Want To Earn Money In Various Ways, Click The Link & Explore Your Field of Interest!!!
Subscribe to:
Comments (Atom)
QR Code Generator:Engineering & Science Calculators: Free Online Tools.
Definition: A *QR code* (Quick Response code) is a two-dimensional barcode that stores data, like text, URLs, or other digital information, ...

-
Definition: An ellipse is the set of all points in a plane where the sum of the distances from each point to two fixed points (called foci) ...
-
Definition: A quadratic equation is a polynomial equation of the second degree, meaning it contains at least one term that is squared. Clic...