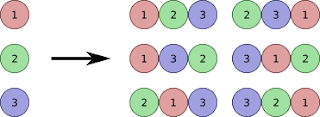
Definition: Permutation and combination are two fundamental concepts in probability and counting problems. A combination is a selection of items from a set, regardless of order.
Click the Translate button(see right) on this post to set your Own Language to understand more perfectly!!
Permutation and Combination Calculator
Permutation and Combination Calculator
Continue Definition:
Permutation and combination are two fundamental concepts in probability and counting problems. Here's a breakdown of each concept with supporting equations and solved examples:
Permutation:
A permutation is an arrangement of a set of distinct objects in a specific order. The order matters, so "ABC" is considered different from "CBA."
Formula:
The number of permutations of n distinct objects (nPr) is calculated using the following formula:
nPr = n! / (n - r)!
where:
n: Total number of objects
r: Number of objects chosen for arrangement
!: Factorial (denoted by an exclamation mark), which represents the product of all positive integers less than or equal to a number (e.g., 4! = 4 * 3 * 2 * 1)
Example:
Imagine you have 3 friends (Alice, Bob, and Charlie) and need to choose 2 of them for a movie night. How many different combinations of 2 friends can you have (considering the order matters)?
Here, n (total objects) = 3 and r (objects chosen) = 2.
Using the formula:
nPr = 3! / (3 - 2)! = 3 * 2 * 1 / 1 = 6
Therefore, there are 6 different ways you can choose 2 friends for the movie night in a specific order (e.g., Alice and Bob, Bob and Alice, etc.).
Combination:
A combination is a selection of items from a set, regardless of order. So, "ABC" and "CBA" would be considered the same combination in this case.
Formula:
The number of combinations of n distinct objects taken r at a time (nCr) is calculated using the following formula:
nCr = n! / (r! * (n - r)!)
where:
n and r are the same as in permutations.
Example:
Let's say you have 4 different flavors of ice cream (Vanilla, Chocolate, Strawberry, and Mango) and want to choose 2 for a sundae. How many different combinations of flavors can you have (regardless of the order you add them)?
Here, n (total objects) = 4 and r (objects chosen) = 2.
Using the formula:
nCr = 4! / (2! * (4 - 2)!) = 4 * 3 / (2 * 2) = 6
Therefore, there are 6 different combinations of ice cream flavors you can choose for the sundae, even though the order of adding them doesn't matter (Vanilla-Chocolate is the same as Chocolate-Vanilla).
Key Differences:
The main difference lies in whether order matters. Permutations consider order, while combinations do not. This is reflected in the formulas:
Permutation formula has (n - r)! in the denominator.
Combination formula has an additional r! in the denominator compared to the permutation formula.
In conclusion:
Understanding permutations and combinations is crucial for solving various counting problems. By using the appropriate formula and considering the importance of order, you can accurately determine the number of possible arrangements or selections for a given scenario.
let's start with the mathematical equations and notation for permutations and combinations:
**Permutations:**
Permutations are arrangements of objects in a certain order. The formula to calculate permutations is:
[ P(n, r) = frac{n!}/{(n - r)!} ]
Where:
( P(n, r) ) represents the number of permutations of ( n ) objects taken ( r ) at a time.
( n! ) denotes the factorial of ( n ), which is the product of all positive integers up to ( n ).
( (n - r)! ) denotes the factorial of ( n - r ).
**Combinations:**
Combinations are selections of objects without considering the order. The formula to calculate combinations is:
[ C(n, r) = frac{n!}/{r!(n - r)!} ]
Where:
( C(n, r) ) represents the number of combinations of ( n ) objects taken ( r ) at a time.
( n! ) denotes the factorial of ( n ).
( r! ) denotes the factorial of ( r ).
( (n - r)! ) denotes the factorial of ( n - r ).
**Questions with solving hints:**
1. **Question:** In how many ways can you arrange 5 books on a shelf?
**Hint:** This is a permutation problem. You want to calculate ( P(5, 5) ).
2. **Question:** How many different 3-letter codes can you make using the letters A, B, C, D, and E?
**Hint:** This is also a permutation problem. Calculate ( P(5, 3) ).
3. **Question:** If a pizza parlor offers 8 toppings and you can choose 3 toppings for your pizza, how many different combinations of toppings are possible?
**Hint:** This is a combination problem. Calculate ( C(8, 3) ).
4. **Question:** A committee of 4 people needs to be formed from a group of 10 candidates. How many different committees can be formed?
**Hint:** This is also a combination problem. Calculate ( C(10, 4) ).
5. **Question:** How many different 5-card hands can be dealt from a standard deck of 52 cards?
**Hint:** This is a combination problem. Calculate ( C(52, 5) ).
**Ways to utilize permutation & combination calculation to earn money:**
1. **Event Planning:** Event planners use combinations to arrange seating plans, menu options, and other arrangements for events like weddings, conferences, and parties.
2. **Stock Trading:** Understanding permutations and combinations can help in a
nalyzing different investment portfolios and predicting stock movements.
3. **Marketing Strategies:** Marketers use permutations and combinations to analyze customer data and develop targeted advertising campaigns, product bundling strategies, and pricing models.
4. **Gaming and Gambling:** Casinos and gaming companies use permutation and combination calculations to design games, set odds, and analyze player behavior.
5. **Software Development:** Permutations and combinations are used in software development for tasks like generating unique codes, passwords, and cryptographic keys.
Do YOU Want To Earn Money In Various Ways, Click The Link & Explore Your Field of Interest!!!