Livestock Heat Stress Index Calculator:Calculators for Students, Engineers & Researchers:free Online Tool

Livestock Heat Stress Index Calculator

Temperature (°C):

Relative Humidity (%):

Soil Erosion Risk Calculator:Calculators for Students, Engineers & Researchers:free Online Tool

Soil Erosion Risk Calculator

Slope (in degrees): Soil Type: Sandy Loam Clay Land Cover: Forest Grassland Cropland Rainfall Intensity (in mm/h):

Soil Erosion Risk:

Pesticide Dosage Calculator:Calculators for Students, Engineers & Researchers:free Online Tool

Pesticide Dosage Calculator

Pest Type: Insect Fungus Weed

Crop Stage: Seedling Vegetative Flowering Fruiting

Desired Control Level: Low Medium High

Livestock Feed Ration Calculator:Calculators for Students, Engineers & Researchers:free Online Tool

Livestock Feed Ration Calculator

Livestock Type: Cattle Sheep Goat Weight (in kg): Protein Requirement (%): Energy Requirement (MJ/kg): Available Feed Ingredients:

Permutation and Combination Calculator:Engineering & Science Calculators: Free Online Tools

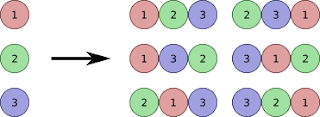
Definition: Permutation and combination are two fundamental concepts in probability and counting problems. A combination is a selection of items from a set, regardless of order.

Click the Translate button(see right) on this post to set your Own Language to understand more perfectly!!

Permutation and Combination Calculator

n:
r:

Continue Definition:

Permutation and combination are two fundamental concepts in probability and counting problems. Here's a breakdown of each concept with supporting equations and solved examples:

Permutation:

A permutation is an arrangement of a set of distinct objects in a specific order. The order matters, so "ABC" is considered different from "CBA."

Formula:

The number of permutations of n distinct objects (nPr) is calculated using the following formula:

nPr = n! / (n - r)!

where:

n: Total number of objects

r: Number of objects chosen for arrangement

!: Factorial (denoted by an exclamation mark), which represents the product of all positive integers less than or equal to a number (e.g., 4! = 4 * 3 * 2 * 1)

Example:

Imagine you have 3 friends (Alice, Bob, and Charlie) and need to choose 2 of them for a movie night. How many different combinations of 2 friends can you have (considering the order matters)?

Here, n (total objects) = 3 and r (objects chosen) = 2.

Using the formula:

nPr = 3! / (3 - 2)! = 3 * 2 * 1 / 1 = 6

Therefore, there are 6 different ways you can choose 2 friends for the movie night in a specific order (e.g., Alice and Bob, Bob and Alice, etc.).

Combination:

A combination is a selection of items from a set, regardless of order. So, "ABC" and "CBA" would be considered the same combination in this case.

Formula:

The number of combinations of n distinct objects taken r at a time (nCr) is calculated using the following formula:

nCr = n! / (r! * (n - r)!)

where:

n and r are the same as in permutations.

Example:

Let's say you have 4 different flavors of ice cream (Vanilla, Chocolate, Strawberry, and Mango) and want to choose 2 for a sundae. How many different combinations of flavors can you have (regardless of the order you add them)?

Here, n (total objects) = 4 and r (objects chosen) = 2.

Using the formula:

nCr = 4! / (2! * (4 - 2)!) = 4 * 3 / (2 * 2) = 6

Therefore, there are 6 different combinations of ice cream flavors you can choose for the sundae, even though the order of adding them doesn't matter (Vanilla-Chocolate is the same as Chocolate-Vanilla).

Key Differences:

The main difference lies in whether order matters. Permutations consider order, while combinations do not. This is reflected in the formulas:

Permutation formula has (n - r)! in the denominator.

Combination formula has an additional r! in the denominator compared to the permutation formula.

In conclusion:

Understanding permutations and combinations is crucial for solving various counting problems. By using the appropriate formula and considering the importance of order, you can accurately determine the number of possible arrangements or selections for a given scenario.

let's start with the mathematical equations and notation for permutations and combinations:

**Permutations:**

Permutations are arrangements of objects in a certain order. The formula to calculate permutations is:

[ P(n, r) = frac{n!}/{(n - r)!} ]

Where:

( P(n, r) ) represents the number of permutations of ( n ) objects taken ( r ) at a time.

( n! ) denotes the factorial of ( n ), which is the product of all positive integers up to ( n ).

( (n - r)! ) denotes the factorial of ( n - r ).

**Combinations:**

Combinations are selections of objects without considering the order. The formula to calculate combinations is:

[ C(n, r) = frac{n!}/{r!(n - r)!} ]

Where:

( C(n, r) ) represents the number of combinations of ( n ) objects taken ( r ) at a time.

( n! ) denotes the factorial of ( n ).

( r! ) denotes the factorial of ( r ).

( (n - r)! ) denotes the factorial of ( n - r ).

**Questions with solving hints:**

1. **Question:** In how many ways can you arrange 5 books on a shelf?

**Hint:** This is a permutation problem. You want to calculate ( P(5, 5) ).

2. **Question:** How many different 3-letter codes can you make using the letters A, B, C, D, and E?

**Hint:** This is also a permutation problem. Calculate ( P(5, 3) ).

3. **Question:** If a pizza parlor offers 8 toppings and you can choose 3 toppings for your pizza, how many different combinations of toppings are possible?

**Hint:** This is a combination problem. Calculate ( C(8, 3) ).

4. **Question:** A committee of 4 people needs to be formed from a group of 10 candidates. How many different committees can be formed?

**Hint:** This is also a combination problem. Calculate ( C(10, 4) ).

5. **Question:** How many different 5-card hands can be dealt from a standard deck of 52 cards?

**Hint:** This is a combination problem. Calculate ( C(52, 5) ).

**Ways to utilize permutation & combination calculation to earn money:**

1. **Event Planning:** Event planners use combinations to arrange seating plans, menu options, and other arrangements for events like weddings, conferences, and parties.

2. **Stock Trading:** Understanding permutations and combinations can help in a

nalyzing different investment portfolios and predicting stock movements.

3. **Marketing Strategies:** Marketers use permutations and combinations to analyze customer data and develop targeted advertising campaigns, product bundling strategies, and pricing models.

4. **Gaming and Gambling:** Casinos and gaming companies use permutation and combination calculations to design games, set odds, and analyze player behavior.

5. **Software Development:** Permutations and combinations are used in software development for tasks like generating unique codes, passwords, and cryptographic keys.

Do YOU Want To Earn Money In Various Ways, Click The Link & Explore Your Field of Interest!!!

Integral Calculator:Calculators for Students, Engineers & Researchers:free Online Tool

Integral Calculator

Function:

Second Order Differential Equation Calculator:Calculators for Students, Engineers & Researchers:free Online Tool

Second Order Differential Equation Calculator

Coefficient a:

Coefficient b:

Coefficient c:

Result:

Algebraic Calculator:Calculators for Students, Engineers & Researchers:free Online Tool

Algebraic Calculator

Geometry Calculator:Calculators for Students, Engineers & Researchers:free Online Tool

Geometry Calculator

Enter the length:

Enter the width:

Trigonometric Calculator:Calculators for Students, Engineers & Researchers:free Online Tool

Definition: A trigonometric calculator is a tool used to compute the values of trigonometric functions for a given angle. Trigonometry itself is a branch of mathematics that deals with the relationship between angles and side lengths in triangles. The most common trigonometric functions are sine (sin), cosine (cos), and tangent (tan).The rest trigonometric functions are Cosec, Sec, & cot. And are the inverse of sin, cos & tan respectly.

Click the Translate button(see right) on this post to set your Own Language to understand more perfectly!!

Trigonometric Calculator

Enter the angle in degrees:

Continue Definition:

A trigonometric calculator is a tool used to compute the values of trigonometric functions for a given angle. Trigonometry itself is a branch of mathematics that deals with the relationship between angles and side lengths in triangles. The most common trigonometric functions are sine (sin), cosine (cos), and tangent (tan)

.

Here's a breakdown of these functions with supporting equations and an example:

Sine (sin): Sine is defined as the ratio of the opposite side (side facing the right angle) to the hypotenuse (longest side) of a right triangle.

Equation: sin(θ) = opposite / hypotenuse

Cosine (cos): Cosine is defined as the ratio of the adjacent side (side next to the angle) to the hypotenuse of a right triangle.

Equation: cos(θ) = adjacent / hypotenuse

Tangent (tan): Tangent is defined as the ratio of the opposite side to the adjacent side of a right triangle.

Equation: tan(θ) = opposite / adjacent

Where, a=opposite, b=Hypotenuse, & c=Adjacent or base.

Example:

Let's consider a right triangle with an angle of 30 degrees (θ = 30°). The opposite side has a length of 6 units, and the hypotenuse has a length of 10 units. We don't have the value of the adjacent side yet.

Using the sine function: sin(30°) = 6 / 10 = 3/5

Using the cosine function (let's find the adjacent side first): cos(30°) = adjacent / 10. We know sin(30°) = 1/2 (using the unit circle or trigonometric tables), so cos(30°) = √(1 - sin²(30°)) = √(1 - (3/5)²) = √(16/25) = 4/5. Therefore, adjacent = cos(30°) * 10 = 4 * 10 / 5 = 8.

Using the tangent function: tan(30°) = 6 / 8 = 3/4

A trigonometric calculator can take the angle value (30° in this case) and the type of function (sine, cosine, or tangent) as input and provide the corresponding trigonometric value (3/5 for sine, 4/5 for cosine, and 3/4 for tangent) as output. Many calculators also offer functions like inverse sine (arcsin), inverse cosine (arccos), and inverse tangent (arctan), which allow you to find the angle for a given trigonometric value.

How to EARN MONEY using Trigonometric Calculator in our practical Life???

Trigonometry has a wide range of applications in practical life that can indirectly help you earn money.

Here are some specific examples:

1. Construction and Surveying:

Land surveying: Trigonometric calculations are crucial for land surveyors to measure distances and angles on a property. They use functions like sine, cosine, and tangent to determine property lines, plot elevations, and calculate areas for construction purposes.

Building design and construction: Trigonometry helps architects and engineers design structures that are stable and functional. They use trigonometry to calculate roof pitches, determine load-bearing capacities, and ensure proper placement of beams and columns. If you're skilled in these areas, your understanding of trigonometry can make you a valuable asset and potentially lead to higher paying jobs or freelance opportunities.

2. Engineering Fields:

Civil Engineering: Similar to construction, civil engineers rely on trigonometry for designing roads, bridges, dams, and other infrastructure projects. They use it to calculate forces, angles, and stress distribution to ensure the stability of these structures.

Electrical Engineering: Trigonometry plays a role in analyzing and designing electrical circuits. It helps engineers calculate voltage, current, and impedance in AC circuits, which is essential for efficient power transmission and distribution. Having strong trigonometric skills can make you a more qualified candidate in these engineering fields, potentially increasing your earning potential.

3. Other Fields:

Animation and Video Game Design: Trigonometry is used in 3D animation and video game design to create realistic movements and trajectories for characters and objects. By understanding angles and distances, animators can create natural-looking movements and game designers can program realistic physics.

Stock Trading (indirectly): While trigonometry isn't directly used for stock analysis, some technical indicators used in trading rely on trigonometric functions. However, a strong understanding of trigonometry isn't essential for success in stock trading.

Earning through Online Platforms:

Freelance Tutoring: If you have a strong understanding of trigonometry, you can offer online tutoring services to students struggling with the subject. Platforms like Upwork or Chegg Tutors allow you to connect with students and potentially earn money by teaching them trigonometric concepts.

Creating Educational Content: You can create online courses or educational content (like video tutorials or ebooks) explaining trigonometric concepts in a clear and engaging way. Platforms like Udemy or Skillshare allow you to sell your courses and potentially earn money by sharing your knowledge.

Remember, while trigonometry itself won't directly earn you money, having a strong understanding of it can be a valuable skill in various fields that do offer earning opportunities. It can make you a more qualified candidate for specific jobs or freelance work, or allow you to create educational content that others can pay for.

Do YOU Want To Earn Money In Various Ways, Click The Link & Explore Your Field of Interest!!!

Programmable Calculator:Calculators for Students, Engineers & Researchers:free Online Tool

Programmable Calculator